Q1b) t-Estimate of the Difference in Two Population Means

ADMS 2320: FINAL EXAM PREP · Winter 2024 2022 Summer Final Q1b) t-Estimate of the Difference in Two Population Means

SOLUTION

In this question, they are asking us to find the 99% confidence interval estimate of the difference in the two population means. There are two different formulas that could be used here, but only one is correct: the Equal Variances t Estimate, and the Unequal Variances t Estimate. In order to choose the correct formula, we must first conduct an F test to check if equal variances can be assumed…

STEP 1 | F-test to check for equal variances:

Given

Toronto: $s_{1} = 97.6964$ , $n_{1} = 7$

Windsor: $s_{2} = 112.5667$ , $n_{2} = 5$

Hypotheses

Null Hypothesis

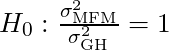$H_0: \frac{\sigma_{\text{MFM}}^2}{\sigma_{\text{GH}}^2} = 1$ (Variances are equal)

Alternative Hypothesis

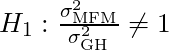$H_1: \frac{\sigma_{\text{MFM}}^2}{\sigma_{\text{GH}}^2} \neq 1$ (Variances are not equal)

Test Statistic

The F-statistic is calculated as:

$F = \frac{s_{1}^2}{s_{2}^2}$

$F = \frac{97.6964^2}{112.5667^2}$

$F = \frac{9545.1926}{12668.9413}$

$F = 0.7534$

Rejection Region

Degrees of Freedom

$df_{1} = n_{1} - 1 = 7 - 1 = 6$

$df_{2} = n_{2} - 1 = 5 - 1 = 4$

Critical Value

The significance level is 0.01 (1%) and it is a two-tailed test.

The upper critical value for $df_{1} = 6$ and $df_{2} = 4$ at this level is 22.0.

The lower critical value is 1/12.0 = 0.0833.

Decision Rule

Therefore, the null hypothesis will be rejected if $F < 0.0833$ or if $F > 22.0$ .

Conclusion

Since the calculated F-value of F = 0.7534 is greater than the lower critical value (0.0833) and less than the upper critical value (22.0), we fail to reject the null hypothesis.

Therefore, we can assume that the variances of the two populations are equal.

STEP 2 | Confidence Interval Estimator for 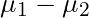$\mu_{1}-\mu_{2}$ When $\sigma_{1}^{2} = \sigma_{2}^{2}$

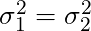
Given

Toronto: $\bar{x}{1} = 35.3676$ , $s_{1} = 97.6964$ , $n_{1} = 7$

Windsor: $\bar{x}_{2} = 30.1875$ , $s_{2} = 112.5667$ , $n_{2} = 5$

Confidence Interval

The 99% confidence interval is calculated as:

$(\bar{x}{1} - \bar{x}{2}) \pm t_{\alpha/2, df} \cdot \sqrt{\frac{s_{p}^2}{n_{1}} + \frac{s_{p}^2}{n_{2}}}$

Degrees of Freedom

$df = n_{1} + n_{2} - 2 = 7 + 5 - 2 = 10$

Critical Value

From the t-distribution table, for 10 degrees of freedom, the critical t-value for a 99% confidence level (two-tailed) is approximately 3.1693.

Pooled Variance

Since we have assumed equal variances, we first calculate the pooled variance:

$s_{p}^2 = \frac{(n_{1}-1)s_{1}^2 + (n_{2}-1)s_{2}^2}{n_{1} + n_{2} - 2}$

$s_{p}^2 = \frac{(7-1)(97.6964)^2 + (5-1)(112.5667)^2}{7 + 5 - 2}$

$s_{p}^2 = \frac{6 \times 9545.1926 + 4 \times 12668.9413}{10}$

$s_{p}^2 = \frac{57271.1556 + 50675.7652}{10}$

$s_{p}^2 = 107946.9208 / 10$

$s_{p}^2 = 10794.6921$

Calculation

$(\bar{x}{1} - \bar{x}{2}) \pm t_{\alpha/2, df} \cdot \sqrt{\frac{s_{p}^2}{n_{1}} + \frac{s_{p}^2}{n_{2}}}$

$(35.3676 - 30.1875) \pm 3.1693 \cdot \sqrt{\frac{10794.6921}{7} + \frac{10794.6921}{5}}$

$5.1801 \pm 3.1693 \cdot \sqrt{1542.0989 + 2158.9384}$

$5.1801 \pm 3.1693 \cdot \sqrt{3700.9373}$

$5.1801 \pm 3.1693 \cdot 60.8399$

$5.1801 \pm 192.6334$

$LCL = 5.1801 - 192.6334 = -187.4533$

$UCL = 5.1801 + 192.6334 = 197.8135$

Conclusion

The 99% confidence interval for the difference in the average hours of watching the sport channel between Toronto and Windsor falls between -187.4533 and 197.8135 hours.

Previous Topic

Back to Lesson

Next Topic

ADMS 2320: FINAL EXAM PREP · Winter 2024

Q1b) t-Estimate of the Difference in Two Population Means

SOLUTION

STEP 1 | F-test to check for equal variances:

Given

Hypotheses

Null Hypothesis

Alternative Hypothesis

Test Statistic

Rejection Region

Degrees of Freedom

Critical Value

Decision Rule

Conclusion

STEP 2 | Confidence Interval Estimator for When

Given

Confidence Interval

Degrees of Freedom

Critical Value

Pooled Variance

Calculation

Conclusion

Leave a Comment Cancel reply

STEP 2 | Confidence Interval Estimator for $\mu_{1}-\mu_{2}$ When $\sigma_{1}^{2} = \sigma_{2}^{2}$