CHAPTER LESSONS - FREE
Chapter 10: Introduction to Estimation
7 Topics | 1 Quiz
Chapter 11: Introduction to Hypothesis Testing
6 Topics | 1 Quiz
2022 Summer Final
9 Topics
CHAPTER LESSONS - PREMIUM
Chapter 12: Inference About a Population
6 Topics | 1 Quiz
Chapter 13: Inference about Comparing Two Populations
7 Topics | 1 Quiz
Chapter 14: Analysis of Variance
3 Topics | 1 Quiz
Chapter 15: Chi-Squared Tests
3 Topics | 1 Quiz
Chapter 16: Simple Linear Regression and Correlation
10 Topics | 1 Quiz
Chapter 17: Multiple Regression:
11 Topics | 1 Quiz
PAST EXAMS - PREMIUM
2021 Winter Final
8 Topics
2021 Summer Final
10 Topics
2020 Fall Final
10 Topics
CHEAT SHEET - PREMIUM
Q3b) F test of the Ratio of Two Variances
SOLUTION
Given
Variance for MFM: ![]()
Variance for GH: ![]()
Degrees of Freedom: ![]() ,
, ![]()
Hypotheses
Null Hypothesis:
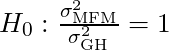
Alternative Hypothesis:
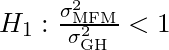
Rejection Region
Critical F-value for one-tailed (lower tail) test at 5% significance level:
![Rendered by QuickLaTeX.com \[ F_{\text{critical}} = \frac{1}{F_{\alpha, df_2, df_1}} = \frac{1}{F_{0.05, 16, 26}} = \frac{1}{2.02} = 0.495 \]](https://statsdoesntsuck.com/wp-content/ql-cache/quicklatex.com-522f955507d97a6b5cd8b9f9361b0fad_l3.png)
F-Statistic Calculation
![Rendered by QuickLaTeX.com \[ F = \frac{s_{\text{MFM}}^2}{s_{\text{GH}}^2} = \frac{0.0562}{0.0330} \]](https://statsdoesntsuck.com/wp-content/ql-cache/quicklatex.com-67284cc427eff5afd9ece22bfb706ab4_l3.png)
![]()
Conclusion
Since ![]() is greater than
is greater than ![]() , we fail to reject
, we fail to reject ![]() . There is not enough evidence at the 5% significance level to conclude that MFM’s variance is significantly less than GH’s.
. There is not enough evidence at the 5% significance level to conclude that MFM’s variance is significantly less than GH’s.
Post a comment