Test – Stats Doesnt Suck

Hypotheses

Null Hypothesis 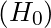$(H_0)$ : The average customer watches 48 hours or less of a sport channel per month. Mathematically, this is expressed as $\mu \leq 48$ .
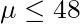Alternative Hypothesis 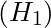$(H_1)$ : The average customer watches more than 48 hours of a sport channel per month. This is expressed as $\mu > 48$ .

Test Statistic

We use the formula for the z-test statistic for a sample mean:

$z = \frac{\bar{x} - \mu_0}{\sigma/\sqrt{n}}$

where:

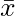$\bar{x}$ is the sample mean, 49.6 hours.
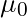$\mu_0$ is the hypothesized population mean, 48 hours.
$\sigma$ is the population standard deviation, 9 hours.
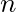$n$ is the sample size, 48.

Calculating the z-value:

$z = \frac{49.6 - 48}{9/\sqrt{48}} \approx \frac{1.6}{1.3} \approx 1.23$

Rejection Region

For a significance level $\alpha$ of 1%, and since this is a right-tailed test (due to $H_1: \mu > 48$ ), we find the critical z-value from z-tables or a standard normal distribution table.

The critical z-value for $\alpha = 0.01$ is approximately 2.33 (since we are looking at the area to the right of the curve).

Conclusion

We compare the calculated z-value with the critical z-value:

Calculated z-value: 1.23
Critical z-value: 2.33

Since $1.23 < 2.33$ , we do not reject the null hypothesis.

Therefore, at the 1% significance level, we do not have sufficient evidence to conclude that the average customer watches more than 48 hours of a sport channel per month. The claim by the Advance cable network that the average customer watches 48 hours or less per month stands.